V.7 #2 Mathematics - Examining the van Hiele Theory: Strategies to Develop Geometric Thought

Brought to you by Learning Disabilities Worldwide (LDW®) through the generosity of Saint Joseph's University.

What makes a rectangle a rectangle? Is a square a rectangle? Is a rectangle a square? These are just some of the many questions which students ponder as they develop levels of geometric thought. Through the study of geometry, students come to understand geometric representations, learn to reason logically, make justifications, build connections among ideas, learn to make sense of their physical environment, develop spatial and location skills, and visualize objects from different perspectives (Jones, 2012). Not only are these geometric understandings essential in and of themselves, but also for the role they play in learning algebra (National Mathematics Advisory Panel, 2008). However, geometry is often underrepresented in the elementary and middle school curriculum (Jones, 2012). Furthermore, mathematics interventions for students with disabilities have focused primarily on number and operations with little attention paid to geometry (Sarama, Clements, Parmar, & Garrison, 2011). It is important for teachers to know the developmental sequence through which children pass as they learn geometric ideas in order to help their students progress from one level to the next. This article highlights the van Hiele Theory of Geometric Thought and some strategies teachers can employ to promote geometric thought at the elementary grade levels with a specific focus on sorting, classifying, composing, and decomposing shapes, and learning properties of shapes.

The van Hiele Theory of Geometric Thought

In the 1950s, a husband and wife team of Dutch educators, Pierre van Hiele and Dina van Hiele-Geldof, developed a theory of how children learn geometry which is still widely accepted today (Jones, 2012). Through their research, they identified five levels of understanding spatial concepts through which children move sequentially on their way toward geometric thinking. A visual image of the van Hiele Theory is shown in Figure 1 and a summary of the van Hiele Theory is presented in Table 1.

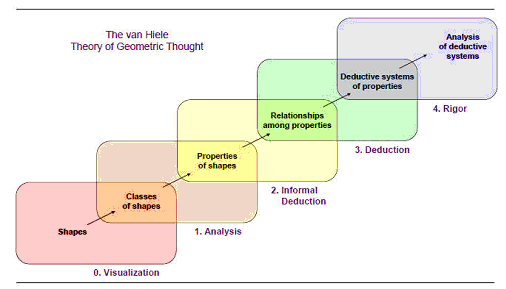
Figure 1. The van Hiele theory of geometric thought. Note. Google Image from www.proactiveplay.com

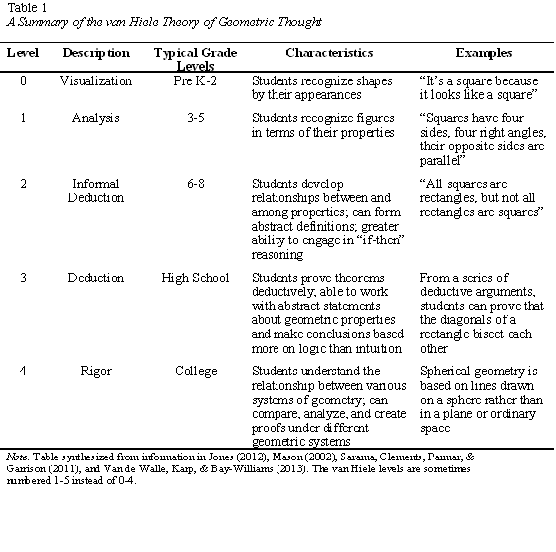
The van Hiele Theory does not explicitly tell teachers how to teach geometry, but can help teachers assess what level their students are working at by looking at some of the characteristics of each level. According to this theory, the geometric levels of thought are sequential; students must move through prior levels to arrive at the next level. However, the levels are not age dependent. Although typical grades associated with each level are shown in Table 1, students may vary at the levels they are at regardless of age or grade. Students also advance through the levels at different rates for different concepts, depending on their exposure to the subject. Geometric experiences are the greatest determining factor influencing advancement through the levels. A child must have enough experiences, either in a classroom or elsewhere, with geometric ideas to move to a higher level of sophistication.

Phases of Geometric Instruction

Since manipulatives can help students with learning disabilities learn mathematics meaningfully (Sarama, Clements, Parmar, & Garrison, 2011), a constructivist approach to teaching geometry is beneficial. One approach is based on the van Hiele Theory in which a student progresses through each level of geometric thought as a result of instruction that is organized into five phases of learning. The van Hieles recommended five phases for guiding students from one level to another on a given topic. Teachers should be aware of these phases and their characteristics, shown in Table 2, in order to aid students in progressing from one level of thought to the next.

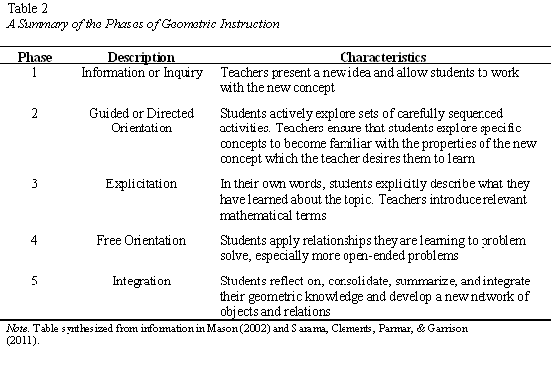
As a consequence of engaging in a series of instructional phases, children will likely have progressed from simply recognizing some shapes, for example, to being able to discuss the shapes in terms of specific geometric properties and perhaps make some comparisons between shapes. Although there are five phases of instruction, it is important for a teacher to consider each phase in relation to their students' characteristics to tailor and differentiate instruction accordingly. Students may need to cycle through some of the phases more than once for a given topic.

Strategies to Develop Geometric Thought at the Elementary Grades

Due to the scope of all that geometry entails at different levels, and because the van Hiele Theory has greatly influenced geometry curricula throughout the world through emphasis on analyzing properties and classification of shapes at early grade levels, this article focuses on some strategies and activities which teachers can use with their elementary students at Levels 0 and 1 to promote sorting, classifying, composing, decomposing shapes, and learning about their properties. For most students with learning disabilities, making links to other disciplines and real-world connections are even more important (Sarama, Clements, Parmar, & Garrison, 2011) and need to be taken into account when planning activities around geometry which emphasizes constructivist approaches.

Level 0. Instruction at this level involves a lot of sorting and classifying. Students need varied opportunities to draw, construct, compose, and decompose shapes in two and three dimensions. Some strategies to promote sorting and classifying and composing and decomposing shapes include:

· Attribute blocks and real-world objects sorts. Provide students with a set of attribute blocks [which typically contain circles, squares, triangles, rectangles, and hexagons in three colors (red, yellow, and blue), two different sizes (large/small), and thicknesses (thick/thin)] and see how students sort them without any parameters given. For a more focused, but still open-ended task, in pairs one student can take a turn to sort and the partner has to guess the rule by which the blocks were sorted (e.g., color, size). To increase the collection of objects beyond attribute blocks, have students sort real-world objects too.

· How are we similar and different? Show students two solids, such as a cube and rectangular prism, and have them describe how the solids are similar and different either orally or in written format.

· Which does not belong? Show students three different solids, such as a cube, cylinder, and rectangular prism, and ask students to identify which does not belong and describe why either orally or in written format.

· Pattern blocks and tangrams. Within an outline of a drawing, have students place appropriate pattern block or tangram shapes to fill the space completely without any gaps or overlaps. In the process, students may discover, for example, that three green pattern block triangles can make one red trapezoid.

· Geoboards. Using geoboards, students can replicate different shapes a teacher shows (perhaps via a card or Smartboard). Students can also record the shapes on geoboard paper.

· Tessellations. A tessellation is a tiling of a plane using one or more shapes in a repeated pattern with no gaps or overlaps (Van de Walle, Karp, & Bay-Williams, 2013). Students can use pattern blocks to create tessellations. Tessellations are also a great way to link mathematics and art as students can explore the work of Escher, for example.

Level 1. Instruction at this level focuses more on properties of figures rather than on simple identification of shapes. The properties are more important than the appearance of the shape. Ideas will apply to entire classes of figures (e.g., all rectangles) rather than on individual models. Students also begin to identify shapes more formally by learning their proper names and their properties. A teacher can stress mathematics vocabulary through use of a word wall. Some strategies to help students focus on properties of shapes include:

· Congruent shapes. A teacher can show students a shape and they have to create congruent shapes on a geoboard.

· 2-D triangle sort. Using varied cut-out triangles, have students sort them by categories: equilateral, isosceles, or scalene.

· 3-D shape construction. Using toothpicks, straws, pipe cleaners, or sticks and some adhesive material such as tape, putty, clay, or marshmallows have students form 3-D shapes. A teacher can specify the number of edges and faces and students have to construct a shape accordingly.

· Who am I? A teacher (and eventually other students) can give clues and students have to guess the name of the figure. For example, "I am a solid with 5 corners, who am I?" or "I am a solid with no faces (no corners), who am I?"

· How would you? A teacher (and eventually other students) holds up a figure and asks students "How would you describe this figure (without giving its name) to someone who has never seen it?"

The aforementioned activities are designed to target a particular level of geometric thought while beginning to advance students to the next level of thought. This article has only scratched the surface of strategies which teachers can employ to promote geometric thought at the elementary grades. Given that mathematics curricula for students with disabilities have not sufficiently emphasized and integrated many aspects of geometry (Sarama, Clements, Parmar, & Garrison, 2011), it is important for teachers to include more geometry in their teaching with a bent toward constructivist approaches. To be able to accomplish this, it is especially important for teachers to understand some of the geometric levels of thought in order to see where students may need greater assistance in order to help them advance to higher levels of sophistication.

References

Jones, J. C. (2012). Visualizing elementary and middle school mathematics methods. Hoboken, NJ: John Wiley & Sons, Inc.

Mason, M. (2002). The van Hiele levels of geometric understanding. Retrieved from http://ebookbrowsee.net/mason-marguerite-the-van-hiele-levels-of-geometric-understanding-2002-pdf-d13505482

National Mathematics Advisory Panel (2008). Foundations for success: The final report of the national mathematics advisory panel. Washington, DC: U.S. Department of Education.

Sarama, J., Clements, D. H., Parmar, R. S., & Garrison, R. (2011). Geometry. In F. Fennell (Ed.), Achieving fluency: Special education and mathematics (pp. 163-196). Reston, VA: NCTM.

Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2013). Elementary and middle school mathematics: Teaching developmentally (8th ed.). Upper Saddle River, NJ: Pearson Education, Inc.

Joan Gujarati, Ed.D., is an Assistant Professor in the Department of Curriculum and Instruction at Manhattanville College in Purchase, New York where she teaches the childhood mathematics methods courses. She is a former elementary school teacher and Math Teacher Leader. Dr. Gujarati has presented at numerous professional conferences and has published in the field of childhood mathematics education. Dr. Gujarati's research interests include early childhood and elementary mathematics education, teacher beliefs and identity, teacher quality, effectiveness, and retention, and curriculum development. Dr. Gujarati can be reached at joan.gujarati@mville.edu